Hoe het gebied van een gelijkbenige driehoek te vinden

Wiskunde en geometrie in het bijzonder, volgensopiniepeilingen van schoolkinderen, een van de meest onbeminde lessen, en allemaal omdat ze je een groot aantal formules leren aanleren die in het leven 90% van de huidige volwassenen nog niet praktisch hebben gevonden. Maar voor een minuut leren we formules, lossen we problemen op, maken we vergelijkingen, niet omdat ze nuttig voor ons kunnen zijn in het leven, maar omdat het denken en logica ontwikkelt. Zelfs de oude Griekse wijzen zeiden dat het menselijk intellect kan worden gemeten door de kennis van de wiskundige wetenschappen. En aangezien u besloot om kennis te maken met de toepassing van de formules voor een gelijkbenige driehoek - houden wij onszelf in de gaten en lezen het hele artikel.
Voordat je begint met het beantwoorden van de vraag hoe te vindenhet gebied van een gelijkbenige driehoek en ga naar het praktische deel van het artikel, waar de formules en berekeningen worden gegeven, laten we het begrip zelf voor onszelf aanduiden. Een gelijkbenige driehoek is een driehoek waarin twee van de drie zijden gelijk zijn in lengte, de zijkanten genoemd. In het geval van een gewone driehoek, waarbij alle zijden gelijk zijn, wordt deze ook als gelijkbenig beschouwd, maar omgekeerd, als een gelijkbenige driehoek als correct wordt beschouwd - is deze onjuist.
De zijkanten van de driehoek moeten worden aangewezen, we zullen het op deze manier doen, zoals weergegeven in de afbeelding hieronder, waarbij: a - zijden, b-basis en h-hoogte.
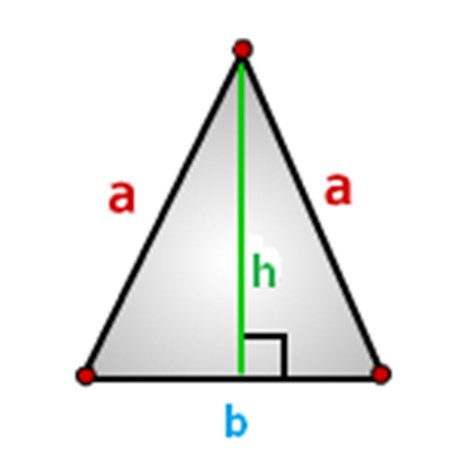
Hoe het gebied van een gelijkbenige driehoek, formules berekenen.
Nadat we de notatie van hoogte, zijden en hoek hebben gemaakt, kunnen we beginnen het probleem op te lossen.
Om te beginnen zullen we bepalen wat we weten.
Als de hoogte en de onderkant - dan is de klassieke formule (* - vermenigvuldigingsteken):
S = ½ * b * h
Laten we de nummers vervangen door bijvoorbeeld: h = 16, b = 18, we krijgen het volgende:
S = 1/2 * 18 * 16 = 9 * 16 = 144;
Het gebied van een gelijkbenige driehoek is S = 144 cm2
Er zijn andere formules die ons zullen helpenin hoe het gebied van een gelijkbenige driehoek te kennen. Eén zo'n formule is de methode van Heron. Laten we geen complexe formule schrijven, we nemen, voor een basis, een verkorte:
S = ¼ b √4 * a2-b2
Het is duidelijk dat b de basis is, en - gelijke kanten. De formule is geschikt in het geval dat h-hoogte onbekend is.
Vervangen van de waarden, laat a = 6, b = 3, we krijgen het volgende:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
U kunt gebruiken om het gebied gelijk aan de zijden van de driehoek en de hoek tussen de zijden te berekenen:
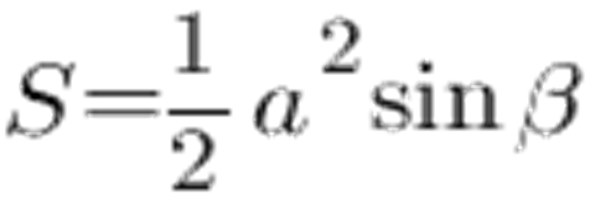
Volgens de sinustafel, de hoek bij 45 ° gelijk aan 0.7071, de zijde a en laat het 6 cm zijn, verkrijgen we het volgende:
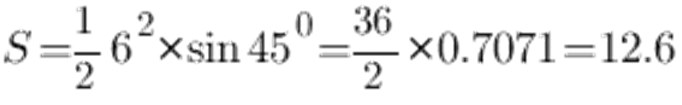
Als gevolg hiervan is de oppervlakte van een gelijkbenige driehoek 12,6 cm2.
Er zijn ook manieren om het gebied te berekenen, inclusiefook in het geval van een gelijkbenige driehoek, maar ze zijn nogal gecompliceerd en niet van toepassing op 'elementaire' berekeningen, zoals die hierboven gegeven, in het begrip complexe wiskunde. En het is niet de moeite waard om over dingen te praten die zelfs docenten met ervaring niet zullen begrijpen.
Dus, je kunt opgelucht ademhaleneen klein geometriecircuit voor het vinden van het gebied van een gelijkbenige driehoek wordt als voltooid beschouwd en de kennis die is verkregen als resultaat van het lezen van het artikel wordt geleerd door "vijf".














